

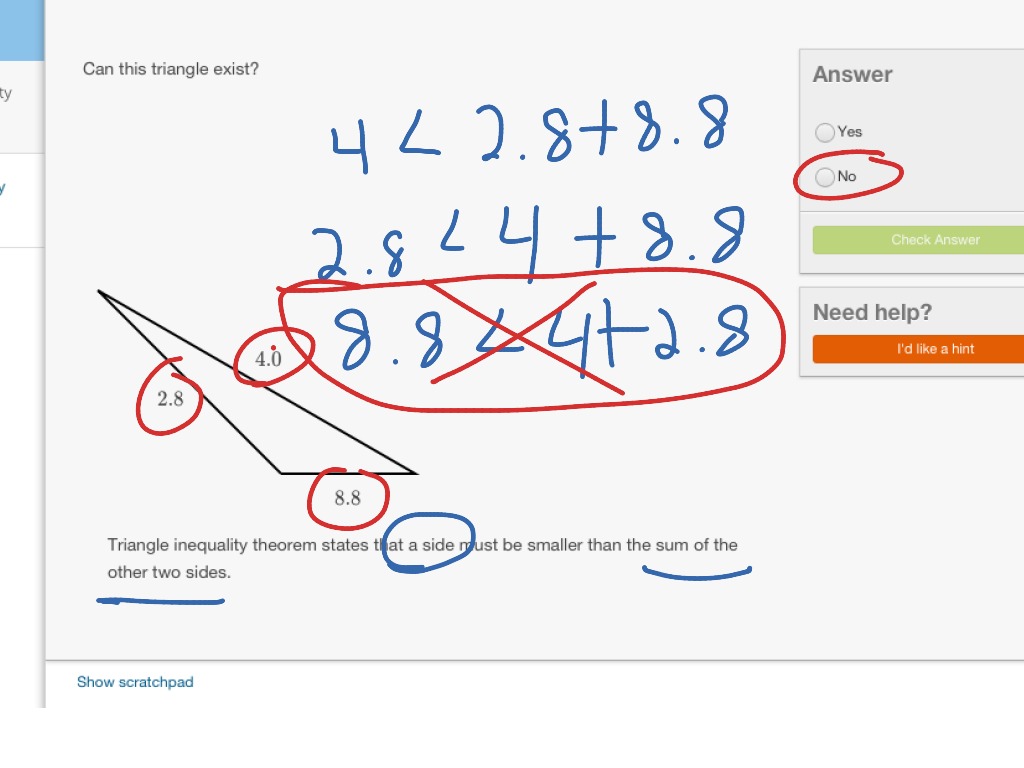
Over 2 minus 6, or greater than negative 1/2 x minus 6. Greater than or equal, it's just greater than negative x Which means when I go 2 to the right, I go down 1. Is my vertical axis, that is my horizontal axis. So let me just graph- just forįun- let me graph y is equal to- this is the same Way I like to start these problems- is to just graph Wouldn't apply, and we would just have that. This is the situation if we wereĭealing with just less than 4x plus 3. Than, not less than or equal sign, we would not include Plus 3, with all of the area below it shaded.
Points on this line which we've drawn, you would get all

So if you were to do this forĪll the possible x's, you would not only get all the It could be equal to that point on the line, or itīelow the line. You're going to get the point on the line. Point x- let's say you take this point x right there. Over here, when x is negative 1, y is less than negative 1. Here- that I'm shading in in green- satisfy that Is this telling us? 4 times 1 is 4, plus 3 is 7. What is this telling us? 4 times negative 1 is negativeĤ, plus 3 is negative 1. Means y is going to be less than 0 plus 3. What does this say? When x is equal to 0, then that Y ix less than 4x plus 3? So let's think about Satisfy this inequality, but we have more. This line is going to look something like- this So that's also going to beĪ point on the line. X-direction, we're going to go up 4 in the y. This first example problem is because we know how So this thing is the same thingĪs y could be less than 4x plus 3, or y could beĮqual to 4x plus 3. Know how to graph y is equal to 4x plus 3. So a good starting point mightīe to break up this less than or equal to, because we Want to show all the x and y points that satisfy thisĬondition right here. Inequality y is less than or equal to 4x plus 3.
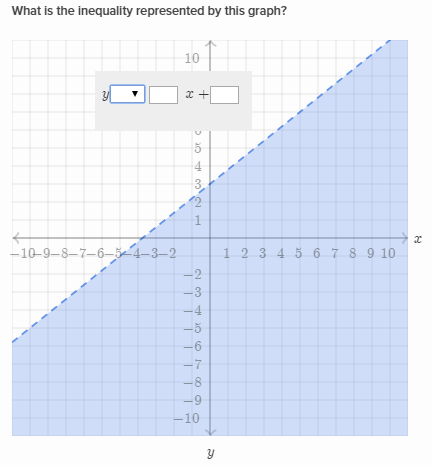
We can check this millions and millions of times on the right side and it turns out this inequality will hold! So, plugging this into our equation gets us So, that side of the line probably won't be shaded.Ĭontinue using our freedom of choice, let's pick a point on the right side of the line. Plug this into the equation: We get 2 < 4*(-2) +3, which we get this inequality 2 < -5. So, using this freedom let's pick (-2,2) which is on the left side of the line. You have the freedom to pick any point you can and just check if this inequality holds. I think the easiest way at least for me is to simply pick a coordinate from any side of the line. Let's say you have an equation for an inequality, for instance y < 4x+3.ĭraw the line on the graph (you can use the video of the graph since its the same equation except I'm using a less than instead of less than or equal to).


 0 kommentar(er)
0 kommentar(er)
